



Above: examples of complex local connectivity that can be achieved entirely using Wang tile constraints.
All of my Wang tile articles and source code can be accessed here.




Above: examples of complex local connectivity that can be achieved entirely using Wang tile constraints.
This article catalogs a large number of possible variations in connectivity when using Wang tiles or herringbone Wang tiles to control connectivity. I intend to write an informal paper with a more technical description of what's going on here that provides a description of the algorithm used to generate this data.
In a "naive" tile set, every room has four corridors going out, one in each direction, and the connectivity is very simple; every room is directly connected to every adjacent room, and, for example, the number of moves (directly from room to room) it takes to get from any room to any adjacent diagonal room is always two.

In illustrations like the above, the white lines show the corridors connecting the rooms; the rooms are the brighter spots at the intersections of corridors (and are just slightly-larger squares). The white lines are not the borders of the tiles (those are present as a much fainter grey). The white lines are not the actual content; they are an abstract stand-in for the real content that allow us to focus on properties of the connecitivity. Real content will be more varied and look less repetitive than these pictures.
On the other hand, making the connectivity data-driven means that the tile set designer has (some) control over connectivity, and different tile sets can have different connectivity behaviors. Or maybe you don't want to (or can't) write the code to do connectivity manipulation. (Note though that you will still have to write/modify the code used to combine Wang Tiles into outputs, as it needs extra constraints to support data-driving it).
It is up to you to decide which of these aspects is more important, or which part of the problem you want to spend more time on.
The "pseudo-connectivity" we'll generate in this paper has the property that every room is connected to every other room, but maybe only indirectly. We can measure how indirect they are by using the right-hand maze-solving rule: keep your right hand on the wall, and walk around. Because the connectivity under consideration isn't maze-like (everything is locally-connected), this rule doesn't solve the maze, but instead returns you to where you started.

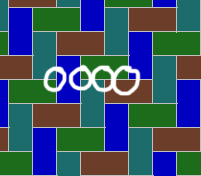
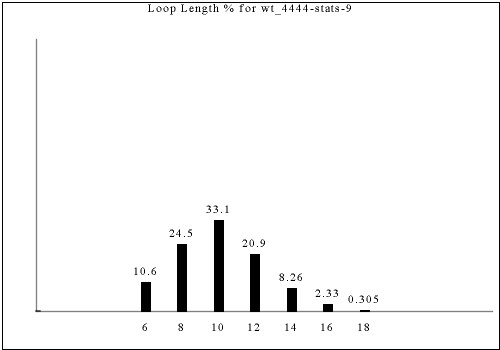
With every room having four corridors to adjacent rooms, it takes 4 moves to return to your starting position. In the example above (rooms are very slightly brighter squares at the meeting between corridors), there are places where it takes 20 moves to complete a full loop returning to the starting location. In fact, we can compute the general distribution of "loop lengths" for any given tileset.

This is the distribution for the dataset shown above.
Note that the percentages show the fraction of total loops that are a given loop length. If you pick a random room in the output and ask how long the loop it's on is, the answer will be different. For example, the graph shows that 16-long loops are slightly rarer than 4-long loops in this dataset, but a 16-long loop reaches 16 different tiles and a 4-long loop reaches only 4 tiles, so a randomly chosen output tile is almost 4 times as likely to be in a 16-long loop as a 4-long loop.
However, it is still useful to preserve the original Wang corner color information, because generating output is a bit easier with Wang corner colors.
Again, the above aren't arguments for corner colors being superior to edge colors, but arguments for why, if you're starting with corner colors anyway, it's worth using them to do the final output synthesis.
As a starting point, consider that regular Wang tiles using edge colors actually have two different kinds of edges--horizontal edges and vertical edges. Assuming you're not rotating tiles during synthesis, the horizontal edges and the vertical edges are unrelated to each other. If you have two colors of horizontal edges and two colors of vertical edges, it doesn't matter what those colors are, the edges are independent. Both horizontal edges and vertical edges can be red & green, or horizontal can be red & green while vertical are blue & yellow, and you'll get the exact same results either way.
The same is not true for Wang tiles using corner colors; there is only one kind of corner, so a 2-color Wang tileset using corner colors really only ever has two colors.
Unlike regular Wang tiles, this is also true of corner colors for herringbone Wang tiles.


As can be seen in the legend at the bottom right of the above image, there are four kinds of corners in herringbone Wang tiles. The previous image shows that the top-left corner of a horizontal tile can only ever meet up with the top-right corner of a vertical tile and the top-middle "corner" of a horizontal tile. If we allow these corners to be colored red and green, then those red and green constraints on the content only affect the three edges adjacent to that corner. If the top-right corner of the horizontal tile is also colored red and green, those red and green constraints don't actually need to affect the edges in the same way as the previous red and green, because those edges never need to meet each other.
Effectively, there are four "corner classes", and it makes no difference if the two colors for each of those classes are the same or are totally different, since they aren't actually shared in practice.
The above image highlights the four different types of corners.
For clarity in illustration, I will always use different sets of colors for each corner type.

The illustration above shows the four herringbone Wang tile corner classes numbered 1-4 and shows how they repeat over the infinite plane.

In the above illustration, I've artificially introduced a simple repetitious pattern for four corner classes for regular Wang tiles. (Other patterns are possible, including more or fewer corner classes, but I chose four for this article for its similarity to herringbone Wang tiles, and to avoid making tile sets get even larger.)
Note that a Wang tile set using 2 colors at each corner with these 4 corner classes can be seen as having no corner classes, but 8 colors and an extra constraint on which colors can be placed at which grid intersections. But I find it easier to understand as there being four different sets of Wang tiles, one for each color of tile in the illustration above (each of which has a different arrangement of the four corner classes). These are different 'classes' of tile, just like herringbone Wang tiles have both horizontal and vertical tiles; we've just introduced four classes of tile that happen to be the same shape.
This also makes it clear that you need 4 times as many tiles as you would for a given number of corner colors. See this section for more details about tile-set tile counts.
The above pattern of corner classes is used for all the Wang tile sets in this article, except for the few very simple ones that use regular Wang tiles.

Each of the tile sets in the catalog are illustrated using an image like the above. Each image shows the result of creating output from a Wang tile set that uses connectivity defined by the legend in the bottom right corner. The four columns in the legend are the four corner classes, and the rows show the different colors for each class. The tile set itself is not shown. Each item in the table shows how a given corner color forces connectivity onto the tiles adjacent to it.
To create a tile set, you must make one tile for every possible combination of the corner colors. The room in each tile must have corridors corresponding to every connection shown for all of the adjacent corners. For example, if the top-left corner requires a vertical connection on its right, then this tile needs a corridor going up; if it also requiers a horizontal connection below it, then this tile needs a corridor going left. Contuning through the corners, if the bottom-left corner requires a horizontal connection above and a vertical connection on the right, then we also must add a corridor going down (the horizontal connection is already handled by the leftward corridor already created).
You can add additional corridors beyond the ones required (i.e. you can derive edge colors, and then arbitrarily choose to make certain edge colors have corridors even if they're not required by the corresponding corners). You can't leave out corridors required by the corner colors without running the risk that your output data won't be fully-connected.
For the last two, not all of the corner classes actually have different connectivity constraints. This allows reducing the number of colors (which reduces the number of tiles that are needed).

In a full Wang tile set with 4 colors, you need 4*4*4*4 or 256 tiles, which is a lot. With the artificial corner classes, you need 4 times as many, or 1024 tiles, which is enough to make 4 corner colors implausible in many contexts.
However, in the above set, while the first corner class (first column) has four different constraints, the second class has the same constraint regardless of color, as does the third (no constraints at all). The fourth class has only two constraints.
Although we typically want at least two colors per class to guarantee some randomness (though it's not actually required!), it does mean we don't actually need to use a full 4 colors for every corner class. Using 4 fior the first class but only two for all the other classes is enough to support all the constraints and produce the same connectivity patterns, but also means we only actually need 4*2*2*2 tiles per tile "type" with four types, or 128 tiles. While still a lot, it's only twice as many as required for 2 corner colors.
The above case is still called "wt-4444" in this catalog, but the table below includes a separate column for limiting the number of colors.
A full table of the number of tiles needed to build a complete set for each of the strategies. To allow comparing the amount of content needed to create herringbone Wang tile sets with regular Wang tiles, each 2x1 herringbone tile is counted as two Wang tiles.
| Strategy | Colors | Number of 1x1 tiles |
|---|---|---|
| wt-4 | 2 | 16 |
| wt-4 | 3 | 81 |
| wt-4 | 4 | 256 |
| hbw-2222 | 2,2,2,2 | 256 (128 2x1 tiles) |
| wt-2222 | 2,2,2,2 | 64 |
| wt-3333 | 3,2,2,2 | 96 |
| wt-3333 | 3,2,2,3 | 144 |
| wt-3333 | 3,3,3,3 | 324 |
| wt-4444 | 4,2,2,2 | 128 |
| wt-4444 | 4,2,2,3 | 192 |
| wt-4444 | 4,2,2,4 | 256 |
| wt-4444 | 4,4,4,4 | 1024 |
Bold entries are used in the catalog.
The above table was computed by hand and may have errors.
These statistics only partially distinguish constraint rules, as some rules with different looking output have the same statistics. Nevertheless, the statistics provide one way of "slicing" up all of the constraint rules we consider here.
The following are all of the distinct statistics found in the catalog for each strategy described in the previous section. Each set of statistics may refer to only one constraint rule or apply to dozens. There is currently no way of viewing the rules that have a given set of statistics except by visually searching for the same graph in the catalog.
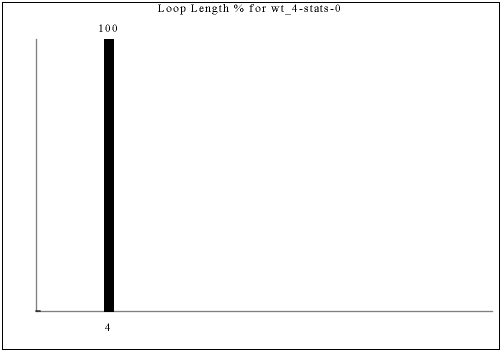








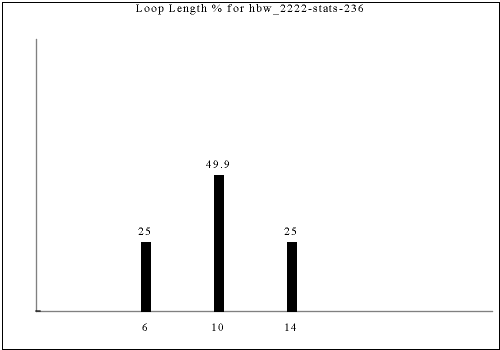

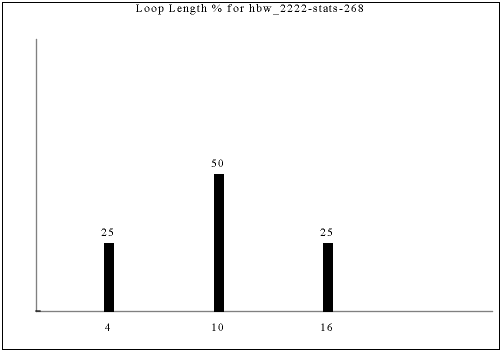



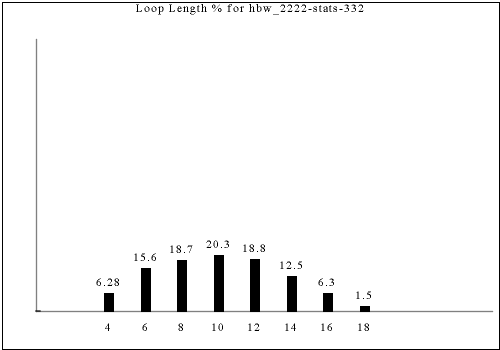



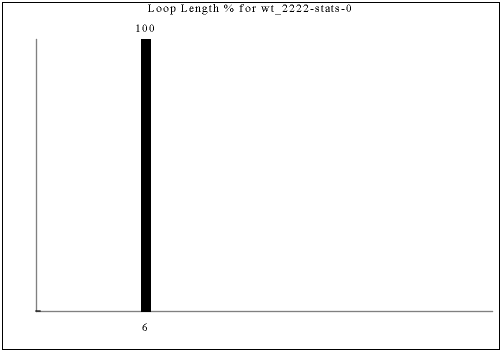

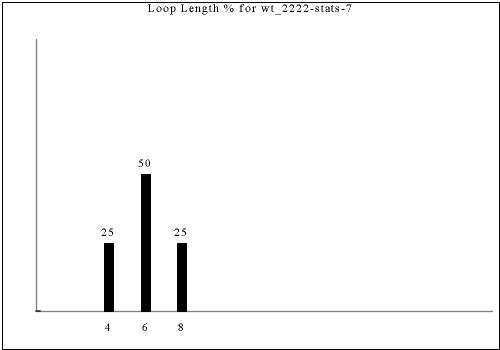

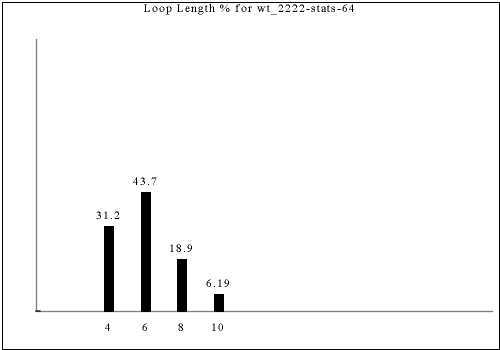
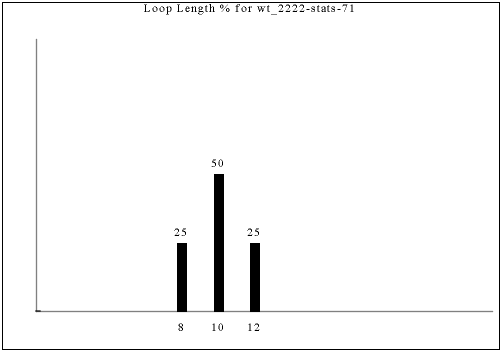
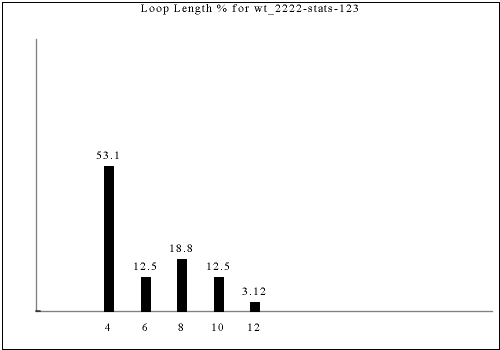
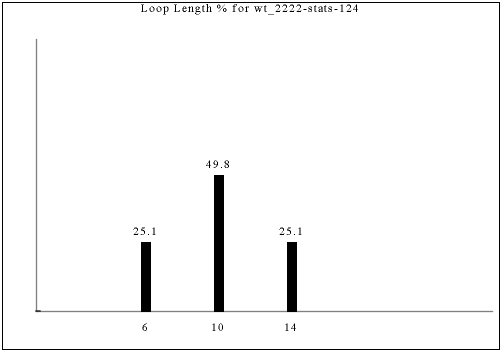

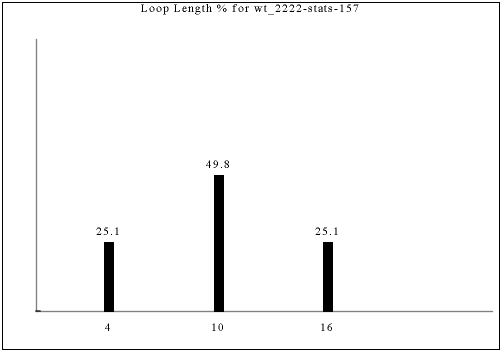
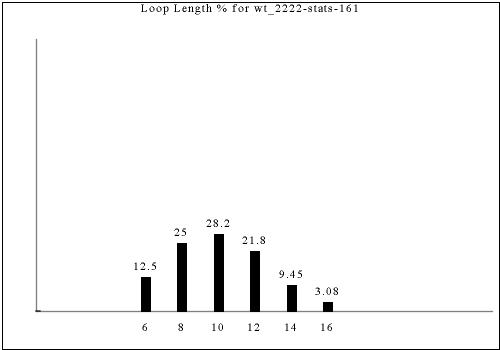

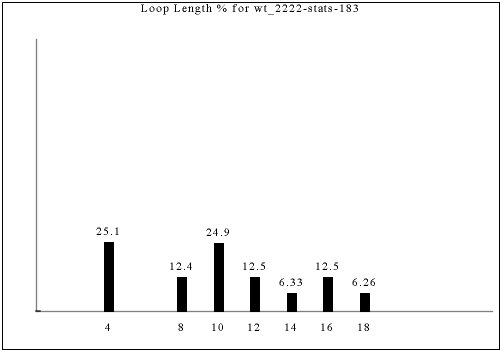
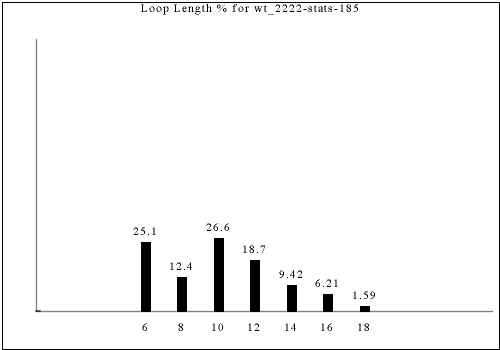

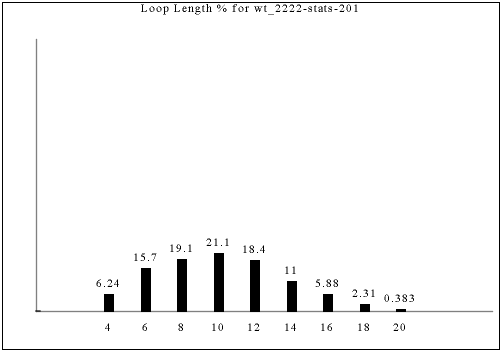


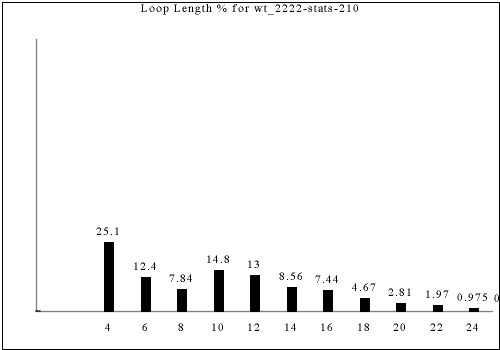

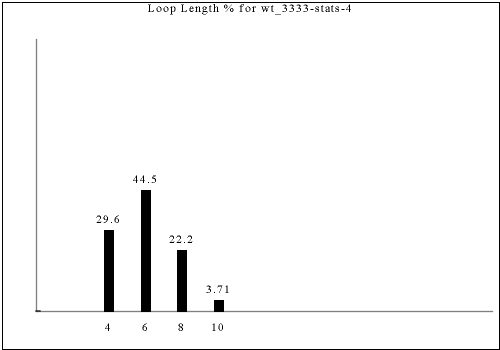


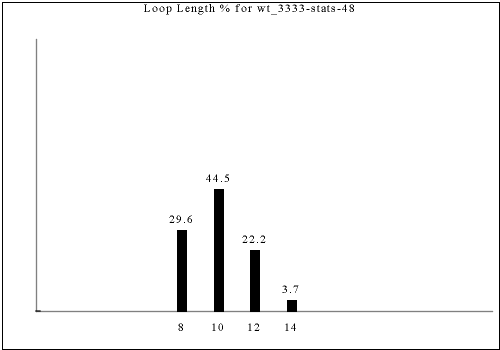







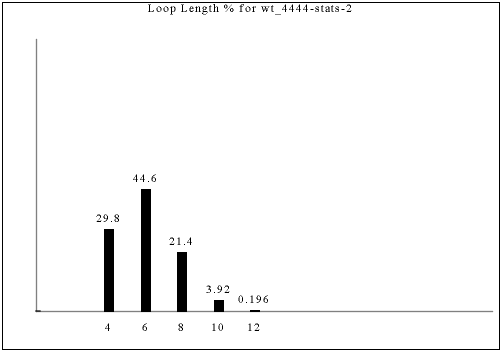



Each of the following images links to the correct place in the full catalog, where you can find brief commentary if you scroll up.
If you're looking for simple, predictable-looking, look at the beginning. If you're looking for complicated, unpredictable-looking, look towards the end.































































































































































































