Herringbone Wang Tiles

This is an unfinished paper that I wanted to get out there. Currently 2011-10-22, originally written in 2010.

Herringbone Tiles
Sean Barrett
Silver Spaceship Software

In this paper I'll describe a method for expanding on the technique of Wang Tiles for generating large 2D regions from smaller ones. I call the technique "Herringbone Wang Tiles" or just "Herringbone Tiles". It is also of particular relevance to the map system used in Infamous by Sucker Punch.

For an unreleased indie CRPG I worked on in 2010, I used an extremely simple method of dungeon map generation. It involves assembling a large map out of small rectangular tiles. Each tile is chosen from a set of 128 pre-authored tiles (each tile is itself made out of small image sprites that are normally called "tiles" as well, but to avoid confusion here I'll call them sprites). The map algorithm is extremely trivial: every tile is selected at random, with no constraints from neighboring tiles or constraints chosen to enforce map connectivity.

The primary technique that made this a viable approach is a novel method for synthesizing large 2D regions from small 2D tiles which I call herringbone tiles, which involves laying out tiles using a herringbone tiling pattern. This technique helps to reduce the obviousness of a regular tiling, and allows better-than-naive connectivity without any computation.

A second technique which I didn't use I call jigsaw colors. Here, we allow the edge shapes of the tiles to vary in certain ways to help break up the long straight edges of a normal tiling. I shall say no more about this in this paper since I didn't try it.

Wang Tiles

The core idea is based on Wang Tiles. It's straightforward to make many small tiles with various edge constraints, and randomly generate a map, placing tiles so that they satisfy the existing edge constraints. (Edge constraints are domain specific; for example, when generating a mostly-solid map with constrained connectivity (e.g. a dungeon), you might say 'for type #1, there's a 10-foot wide passage at the center of the edge'. You might also have constraints on other properties, such as rendering properties, altitude, etc.)

With square Wang Tiles, you can use a trivial left-to-right, top-to-bottom generator. At each step you have to satisfy (at most) two edge constraints when choosing a tile (that is, the constraints are that it must match the two already-generated tiles it abuts). If you have two colors of edges (two possible edge constraints for each edge), you have four cases of constraints to match. As long as you have at least one tile for each case, you can automtaically generate a tiling.

However, you need more than one tile for each case to avoid reptition.

One theory to consider is that for "best" results, you should have enough tiles for each case that you can have every possible combination of "output" edges; this limits the choice of tile at a given location to only influencing its immediate neighbors; the choice can have no effect on tiles further away. With two edge variations (colors) per edge type, that means a minimum of 16 pre-authored tiles. With three edge variations, that's a minium of 81 tiles, which may seem excessive. I'll call such a collection of tiles a "complete stochastic set".

The canonical paper on this method of Wang Tile usage, Wang Tiles for Image and Texture Generation (Cohen et al), uses only 2 tiles per constraint case; e.g. with three edge variations/colors, so 9 total cases, they use only 18 tiles. They do not make any particular argument why this is sufficient for good visual results, nor do they provide any mechanism for how to construct a "good" set of tile color patterns for a given number of constraints. Obviously 2 tiles at each step guarantees you have some random choice, and this guarantees a non-periodicness, but it's not necessarily minimal, nor is it immediately obvious how to choose a good set of "output" edge colors for each variation to guarantee a good distribution of the content.

By comparison, the complete stochastic set proposed above needs no design process to determine what color sets to use (one must construct exactly one preauthored tile for every possible combination of constraints), so while it has the disadvantage of needing a lot more content, it has the advantage of not requiring this undefined design process.

Large Tiles

Sometimes it might be useful to put "special content" into a Wang Tile system, where that content is larger than a single tile. For textures, this could be some special-appearing unique ground formation; for city generation this might be a large convention center which covers more than a normal city block; for a dungeon it might be a large cavern. Such a special region would cover the same area as some number of tiles; it might be 2x1 tiles, 1x2 tiles, 3x4 tiles, or even erratically shaped.

It is trivial to handle such things within the Wang Tile formalism; given, say, a 2:1 sized-rectangle, split it into two squares, and introduce a new, unique color at the boundary between the two squares. Now if you place one of the squares, the only way to complete the tiling is to place the other square next to it.

However, while this works within the formalism, it doesn't work with the simple stochastic generator described above. Once you place the first square, you've placed a unique constraint on the adjacent square, but there's already another constraint on that square already from the previous row of tiles. If the authored second square doesn't match the pre-existing constraint, there is no way to complete the tiling generated so far.

One solution to this would be to then require multiple variations of the second square; if there are three possible edge constraints on each edge, then you would need three variants of the second square. Given that the intent here is to author special "one time only" content, this seems like a significant burden, but it might be viable in some contexts.

A second approach is to step away from placing the large tiles using the formalism. Instead of generating in a trivial left-to-right, top-to-bottom order, we can place the "special" large tiles first, before doing anything else. (Since they're not placed by the normal Wang Tile process, you do not need to bother introducing special colors to guarantee they are generated next to each other; simply directly place them.) Then fill in the rest of the map with a valid tiling that meets the already-placed constraints.

It is not clear how one could write an efficient solver that could satisfy the existing constraints and produce a valid tiling, since the general tiling problem is NP-complete (???). The "stochastic" Wang Tiling approach defined above only worked because there were no additional constraints, by design.

However, if you use the complete stochastic set, the filling algorithm is trivial, because we guarantee that we have a tile that can match every possible constraint on every combination of edges. So you can go back to filling left-to-right, top-to-bottom, and you just have to make the generator be aware of additional constraints that have been placed by the pre-generated special tiles.

For this reason, I believe that complete stochastic set tiling is actually an important and worthwhile approach to implementing Wang Tiles; despite the obvious triviality of the method, I'm not aware of any prior discussion of the benefits in the literature, which, to sum up, are:

guarantees tile choices don't have influences further than one neighbor
trivially supports pre-placement of regular tiles and large tiles before stochastic generation

The drawback is the large amount of content required (e.g. 16 tiles for 2 edge constraints, and 81 tiles for 3 edge constraints). Still, the complete stochastic set is thus particularly worth using if the amount of content it requires is in the same ballpark as the amount of content you wanted to generate anyway; if you make sure you make a complete stochastic set you gain the above advantages. (E.g. if you thought you wanted about 64 pre-authored tiles with 3 edge constraints, just make 81 instead.)

Rotation

It's also possible to allow tile rotation or mirroring. However, this complicates the nature of the edge constraint; with 90-degree rotation, the edge constraints on horizontals must be the same as the edge constraints on verticals. If mirroring (or 180-degree rotation) is allowed, the edge constraints must be internally symmetric. The advantage is that if rotation or mirroring are allowed, the minimum number of tiles needed decreases. (I haven't done the math to explore how far it goes down; somebody should.)

Issues with Wang Tiles

When generating maps or data with Wang Tiles, some artifacts may be visible. One artifacts arises from the grid layout; edges are adjacent to each other in a straight line, so if the edges have particular features or are particularly biased, that straight line may easily be visible when zoomed out. For example, in my application, more of the area of the map is open than closed, but edges are mostly closed. This leads to an obvious grid of "higher density of closedness" with Wang Tiles.

A second issue for my application involves map connectivity. If each edge constraint controls how "corridors" connect between tiles, and we limit ourselves to small enough tiles that we can have only one corridor per edge, then we have two connectivity issues: tracking how edges connect internally, and tracking that the overall map is fully connected.

We can make all tiles always fully-connected internally, so that we don't have to track those specially. Then we know that a map is always fully-connected, but at this point it's too homogenously connected to be interesting. We can address this by having one of the edge constraint types be "not connected". (This increases the number of tiles we need.) Then we can use some kind of global connectivity tracking algorithm when generating to make sure everything stays connected; for example some kind of maze generation algorithm.

Hexagonal Tiles

Another possibility is to use hexagonal tiles, as in the game Infamous by Sucker Punch; see Building an Open-World Game Without Hiring an Army by Nate Fox, e.g. here. (Link revised 2011-10-24, and again 2018-01-18.)

With hexagonal tiles, when doing random generation three edges are constrained and three edges are free choices. With non-rotated tiles and only two edge variations per edge type, this requires 8 cases and 16 tiles, or 64 tiles for the complete stochastic set. (For Infamous, Sucker Punch presumably allowed rotation and appear to have had more than four edge constraints, but they were assembling by hand so were able to limit the number of pre-authored tiles by making careful choices.)

Herringbone Tiles

For my unfinished 2010 CRPG, I attempted to address the issues mentioned with Wang tiles by developing a new variation which I call herringbone tiles.

Herringbone tiles use rectangles with a horizontal-to-vertical ratio of 1:2 and 2:1. Both kinds of rectangles are used in the tiling.

The following illustration shows the general herringbone pattern for rectangles with a 2:1 ratio:

Note that in this pattern, the edges of rectangles touch edges of other rectangles in a consistent way; the top of the right edge of a vertical rectangle always abuts the left edge of a horizontal rectangle; the bottom of the right edge of a vertical rectangle always abuts the top left edge of a vertical rectangle.

As a result, we can distinguish 6 kinds of "edge matchups" that behave in a consistent way, similar to the horizontal and vertical edge types in Wang Tiles. In fact, herringbone tiling is isomorphic to hexagonal tiling; in fact, each rectangle can be seen as a hexagon whose edge lengths are held fixed but whose corners are flexed so that two opposite corners are straightened out to 180 degrees and the remaining corners squeeze down to 90 degrees. There are is reduced while the perimeter remains the same (the rectangle effective has six equal-length edges, if you split the long edges, just like the hexagon).

The square has two distinct edge orientations (horizontal and vertical), and the hexagon has three distinct edge orientations (say, horizontal, 120-degrees left, and 120-degrees right). The herringbone tile has six distinct edge "orientations", because the mix of horizontal and vertical tiles makes the matchups more distinct.

Nevertheless, each tile only has six edge (splitting the long edges in two), so the number of tiles needed to be able to do random generation is still equivalent to that for hexagons, but doubled for the two orientations of tiles.

To do Cohen-et-al-style tiling with two edge types, you have 8 cases (three constrained edges), so you need 16 horizontal tiles and 16 vertical tiles. A complete stochastic set requires 64 horizontal tiles and 64 vertical tiles. These numbers are twice the size of a hexagonal tiling, so it might be worth pursuing rotation to reduce the counts; however, I haven't investigated this myself, as my CRPG used 64 horizontal tiles and 64 vertical tiles, as this was around the amount of unique content I wanted anyway.

Here are the 128 pre-defined content pieces I used to build the dungeon.

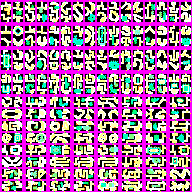
Each edge has two possible cases (a wide corridor or a narrow corridor), but it turned out it looked ok at this resolution to allow the wrong types to match each other, so the constraints are actually ignored. (Had I placed them in diffeerent locations on the edge, this wouldn't have worked.)

Here is an example view of a dungeon generated from this herringbone tile set (zoomed out much much farther than a player would see):

There is additional variety in this because the content pieces have some procedural elements (placement of furniture, floor tile coloration).

Also you can see that it's extremely incoherent, since there's no planning or structure to anything. (This would be less obvious to a player with a much more limited view, but also doesn't really matter for the style of game this was designed for.)

But there are a few positives things worth noticing:

Although you can find long edges which are wall-ish, they don't come out too uniformly. This is because the tile edges are broken up by the herringbone pattern.
The overall connectivity between areas is complicated.

It's not hard to write a dungeon generator with complicated connectivity, but, again, this dungeon generator simply selected every tile randomly independently of every other tile.

The connectivity arises from a trick using the herringbone pattern: each tile is thought of as two squares, and all the outward-facing edges of each square are internally connected to the other edges of the same square; the interior edge between the two squares may or may include a connection between the two squares. (Additional variation then arises by pushing the "contents" of one square or the other over the middle of the boundary between the squares, while the other square is squished down; you can see an example of this in the top-left-most tile in the original tile set. This breaks up the horizontal edge that it aligns with.)

If no internal connection occurred, the connectivity would look like this:

Note that this guarantees full connectivity (no unreachable content is generated), yet sometimes requires roundabout paths to get from one point to another.

This technique might also be of use in for something like Infamous's city; one of the observations made in the presentation linked above was that the hexagonal tiles were a poor match for street grids, which are normally rectangular. Since Herringbone Tiles with rotation appear to be somewhat isomorphic to hexagonal tiles, they might support an approach involving a similar amount of design work and content but yield streets that have rectangular grids.

Edit 2011-10-24: Won Chun reminds me about Colored corners, an alternative formulation for constraints that should give higher quality corner matches for the same amount of content, and is also applicable to herringbone tiles. Didn't matter for my CRPG since I didn't use constraints in the end.