A Catalog of Wang Tile Corner-Color Constraints Controlling Connectivity
Sean Barrett (@nothings)
Silver Spaceship Software
2017-06-27

Index and details are here.

The various kinds of connectivity are mostly organized by properties of the shapes of the "connectivity loops" described previously. Additionally, some sets are described by the orientation of dead-ends in their tile-sets. (A dead-end in this context is a 1x1 tile which has only one corridor leading to it.)

In each of the sample images shown, the legend shows the corner constraints necessary to generate the tile-set, not the actual tile-set. See section 4 for details. The strategies needed (such as "wt-2222") are described in section 5.

There are many duplicates because the software that generated the data only eliminated duplicates and symmetries from the constraint rules, not from the final tile sets. The duplicates are included in the catalog in case I made any mistakes while hand-classifying them.

The catalog is arranged as follows:

If you're looking for simple, predictable-looking, look at the beginning. If you're looking for complicated, unpredictable-looking, look towards the end.

Periodic

Trivial

wt-4


wt-2222


Brick pattern

A brick pattern in the connectivity loops can be achieved with both Wang tiles (wt-2222) and with herringbone Wang tiles (hbw-2222).

wt-2222


hbw-2222


Herringbone pattern

A herringbone pattern in the connectivity loops can only be achieved using herringbone Wang tiles (hbw-2222).

hbw-2222


The following variation is the one used in the first herringbone Wang tile article, as connectivity is never forced through the middle of the 2x1 tiles, allowing every tile to choose for itself, independent of all Wang constraints, whether to add additional connectivity.

Tetris pieces

All tetris pieces can be tiled in some simple periodic pattern on the plane. It turns out that for every tetris piece except the "T", there is some corner color constraint set that will produce connectivity shapes consisting of that tetrris piece tiled on the plane. Of course they all have the same trivial stats shown above.

wt-2222

The 2x2 Tetris piece appears in connectivity loops with an interior dead-end. The tile set can have either 1 or 2 directions of dead-ends.

hbw-2222



Split tetris piece

There are also some simple tilings which consist of a tetris piece split into two chunks, but then a simple strict tiling that follows the tetris piece tiling.

wt-2222

hbw-2222


Near-periodic

Minor variation from naive Wang tiles

These are the only non-trivial connecivity that can be achieved with plain Wang tiles, that is, without introducing corner classes. They require at least three corner colors (which means 64 tiles in the set).


The following requires four corner colors (256 tiles in the set), allowing the output to omit both vertical and horizontal edges instead of only one as in the previous type. Note that this is essentially the same amount of tile content required to author a herringbone Wang tile set, which can have much, much more complicated connectivities.

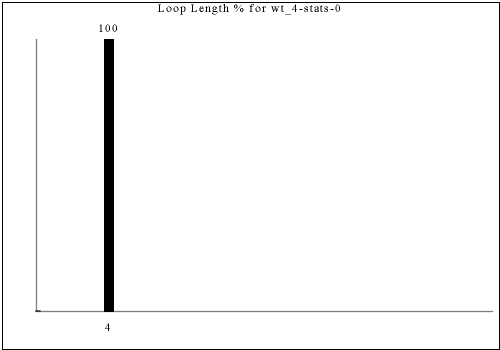
Repeating element every 2x2 cluster

wt-2222

A 4-move (1x1) loop appears every 2x2 tiles:



There are square waves horizontally repeating every 2 columns, duplicated every two rows:


Infinite lines

In all of the variations in this section, there are unbroken horizontal or vertical lines of connectivity spaced either every 1 or every 2 columns or rows. There are many very different variations with this property.

hbw-2222


wt-2222









wt-3333





Tetris-piece-dominated tilings

hbw-2222

In each of the following tilesets , the loops form a Tetris piece (made of four 1x1 pseudo-tiles) which is intermixed with two other shapes (one made of two or three pseudo-tiles, the other of five or six).




Complex variation from Tetris tilings

The tilings below include two mirrored versions of a Tetris piece, or two different Tetris pieces, along with a 3-pseudo-tile loop and a 5-pseudo-tile loop

wt-2222


hbw-2222








As above, but the extra shapes are made of 1 and 7 pseudo-tiles.


Weakly Tetris

hbw-2222

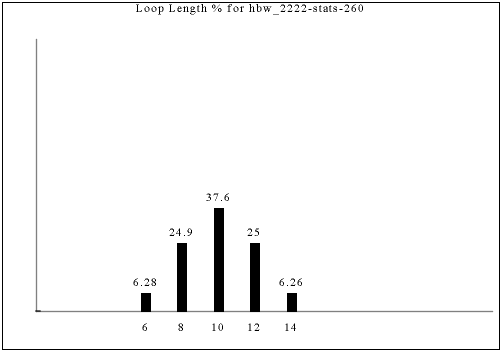
The connectivity loops for the following tilings each prominently include two or more Tetris pieces, along with two smaller and two larger shapes.




Recurring 2x2 pattern

The connectivity loops in the following tilings are dominated by a 2x2 pattern which appears frequently but not always. (It could also be a member of the earlier section on Tetris variations, or the following section.)



Very long lines

The "infinite lines" section includes tilings which have infinite lines on either the horizontal or vertical axis. This section includes tilings which have similar features, but are broken up occasionally.

hbw-2222


wt-3333



wt-4444

Non-periodic

No dead-ends

Axially biased

These tilesets show a strong bias towards either the horizontal or the vertical.

hbw-2222


Brick biased

hbw-2222

The following tilesets show a strong bias towards a brick pattern or a herringbone pattern.






Diagonally biased

hbw-2222

These connectivity graphs show a strong diagonal bias, and feature a high frequency of 1x1 loops.


Miscellaneous

hbw-2222

These were left after all the other classificationsw ere made.




Simple shapes

Each of the following variations uses between 3-5 relatively smiple shapes.

wt-2222


wt-3333




With dead-ends

The various tilesets found here have either one, two, or three directions of dead-ends. No tileset has dead-ends oriented in all four directions. This creates a directional bias that may be objectional in some contexts.

We distinguish first based on the frequency with which dead ends occur.

(It might be more useful to classify how many unique dead-end tiles there are in the tilesets, but I didn't compute that.)

Dead-ends, one direction

























Dead-ends, two directions (adjacent)

Dead-ends, two directions (opposite directions)

Dead-ends, three directions







Many dead-ends, one direction






Many dead-ends, two directions (opposite)


Double dead-end

In this category of tilesets, there are herringbone tiles in which the dead-end occurs in one half of the tile, and the path to the dead-end comes from the other half of the tile and itself has only one entrance.

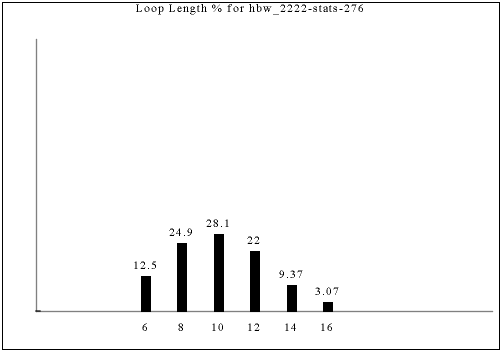
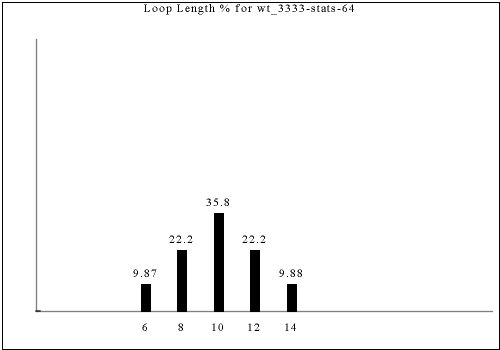
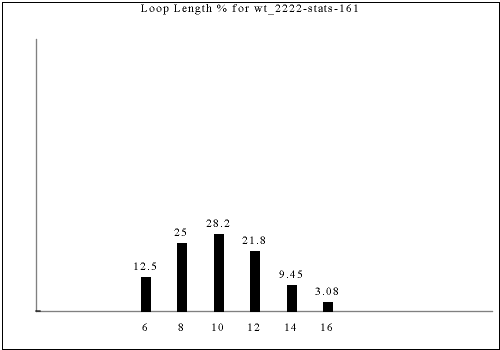
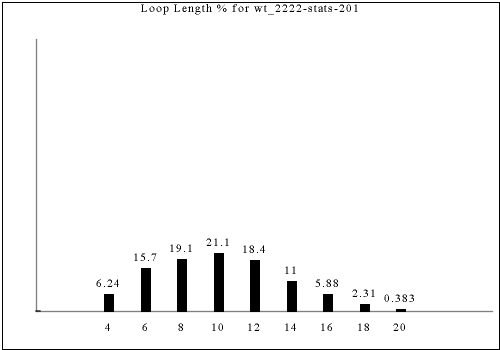
Other tilesets generate these two-long dead-ends, but the following tilesets are unique because the double dead-end occurs within a single herringbone tile, allowing the tile content to be fully tailored knowing it is a double dead-end; in other tile sets, only one of the two 1x1 tiles participating in a double dead-end--the one with the real dead-end--is known in advance to be a double-dead end.




up